Functions

\(\begin{aligned}&\text{The graph of a polynomial function }y=f(x)\text{ in the }x\text{y-plane passes through the point }(3,5).\\&\text{What is the value of }f(3)?\end{aligned}\)

\(\begin{aligned}&\text{The graph of a polynomial function }y=f(x)\text{ in the }xy\text{-plane passes through the point }(8, 9).\\&\text{What is the value of }f(8)?\end{aligned}\)

\(\begin{aligned}&\text{The graph of the polynomial function }f\text{ in the }xy\text{-plane, where }y=f(x)\text{, has }x\text{-intercepts of}\\&(-5,0)\text{ and }(6,0).\text{ Which of the following must be true?}\end{aligned}\)

\(\begin{aligned}&\text{The graph of the function }f\text{ in the }xy\text{-plane, where }y=f(x),\text{has }x\text{-intercepts of}\\&(-5,0),~(3,0)\text{, and }(6,0)\text{. Which of the following must be true?}\end{aligned}\)

\(\begin{aligned}&\text{The function }F(m)=7m\text{ models the force, in newtons, acting on each object in a certain}\\&\text{field as a function of the object’s mass }m,\text{in kilograms. Which statement is the best}\\&\text{interpretation of }F(4)=28\text{ in this context?}\end{aligned}\)

\(\begin{aligned}&~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~p(v)=150v\\
&\text{The function }p\text{ gives the relationship between the instantaneous power }p(v),\text{ in watts, }\\&
\text{and the potential difference }v,\text{ in volts, for a current of 150 amperes. Which statement}\\
&\text{is the best interpretation of }p(3)=450\text{ in this context?}\end{aligned}\)

\(\begin{aligned}
&\text{The function }f(w)=6w^{2}\text{ gives the area of a rectangle, in square feet (ft }^2),\text{ if its width is }w\text{ ft and}\\
&\text{its length is 6 times its width. Which of the following is the best interpretation of }f(14)=1,176?
\end{aligned}\)

\(\begin{aligned}&\text{The kinetic energy, in joules, of an object with mass 9 kilograms traveling at a speed of }v\\
&\text{meters per second is given by the function }K\text{, where }K(v)=\frac{9}{2}v^{2}.\text{ Which of the following }\\
&\text{is the best interpretation of }K(34) = 5,202\text{ in this context?}
\end{aligned}\)

\(\begin{aligned}&~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~k(x)=-\frac{1}{2}x^2+8x+20\\
&\text{The function }k\text{ gives the estimated number of students in a school organization }x\text{ years}\\
&\text{after the organization was established, where }0\leq x\leq10.\text{ Which statement is the best}\\
&\text{interpretation of }k(4)=44?\end{aligned}\)

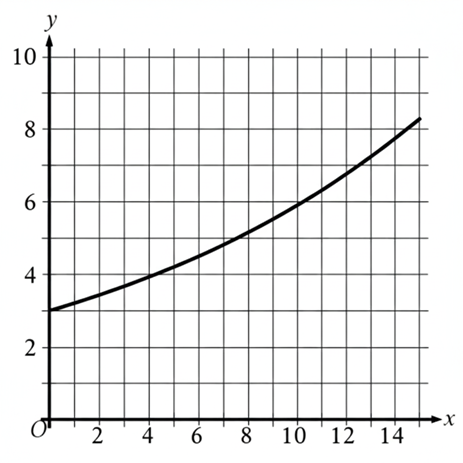
\(\begin{aligned}
&\text{The graph models the population, in thousands, of a town }x\text{ years since 2004, where}\\
&0<x<15.\text{ Which statement is the best interpretation of the point }(1,3.21)?\end{aligned}\)

\(\begin{aligned}&~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~f(x)=x+\frac{8}{11}\\
&\text{The function }f\text{ is defined by the given equation. What is the value of }f(x)\text{ when }x=\frac{3}{11}?\end{aligned}\)

\(\begin{aligned}
&\text{The function }d\text{ is defined by }d(x)=200-6^x.\text{ What is the value of }d(0)?
\end{aligned}\)

\(\begin{aligned}&\text{The function }f\text{ is defined by the equation }f(x)=7x+2.\text{ What is the value of }f(x)\text{ when}\\&x=4?\end{aligned}\)

\(\begin{aligned}
&\text{The function }f\text{ is defined by }f(x)=4x.\text{ For what value of }x \text{ does }\\
&f(x)=8?
\end{aligned}\)

\(\text{The function }f\text{ is defined by the equation }f(x)=4x-3.\text{ What is the value of }f(10)?\)

\(\begin{aligned}&\text{The function }f\text{ is defined by }f(x)=8x.\text{ For what value of }x\text{ does }\\&f(x)=72?\end{aligned}\)

\(\text{The function }f\text{ is defined by }f(x)=x^2+x+71.\text{ What is the value of }f(2)?\)

\(\begin{aligned}&\text{The function }g\text{ is defined by }g(x)=6x.\text{ For what value of }x\text{ does }\\&g(x)=54?\end{aligned}\)

\(\text{The function }f\text{ is defined by }f(x)=-5x^2-7.\text{ What is the value of }f(-1)?\)

\(\begin{aligned}&\text{The function }p\text{ is defined by }p(n)=7n^3.\text{ What is the value of }n\text{ when }\\&p(n)\text{ is equal to }56?\end{aligned}\)

\(\begin{aligned}
&\text{The function }f\text{ is defined by }f(x)=\frac{x+11}{3},\text{ and } f(a)=16 \text{, where }a\text{ is a constant.}\\
&\text{What is the value of }a?\end{aligned}\)

\(\begin{aligned}
&~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~f(x)=x^3+8x+17\\&\text{For the given function }f,\text{the graph of }y=f(x)\text{ in the }xy\text{-plane passes through the point}\\&(0,b),\text{ where }b\text{ is a constant. What is the value of }b?\end{aligned}\)

\(\text{The function }f\text{ is defined by }f(x)=8x^3+4.\text{ What is the value of }f(2)?\)

\(\begin{aligned}&\text{The function }g\text{ is defined by }g(x)=10^{3x-1}.\text{ What is the value of }x\mathrm{~when~}\\&g(x)\text{ is equal to}\text{ 10,000?}\end{aligned}\)

\(\text{The function }h\text{ is defined by }h(x)=5|x|.\text{ What is the value of }h(-3)?\)

\(\begin{aligned}&\text{The function }f\text{ is defined by }f(x)=8\sqrt{x}.\text{ For what value of }x\text{ does }\\&f(x)=48?\end{aligned}\)

\(\text{The function }f\text{ is defined by }f(x)=\frac{1}{2}(x+6).\text{ What is the value of }f(4)?\)

\(\text{The function }h\text{ is defined by }h(x)=\frac{8}{5x+6}.\text{ What is the value of }h(2)?\)

\(\begin{aligned}&\text{The function }g\text{ is defined by }g(x)=x^2+9.\text{ For which value of }x\text{ does }\\&g(x)=25?\end{aligned}\)

\(\begin{aligned}&\text{The function }w\text{ is defined by }w(r)=\frac{1}{r-8}-\frac{r-5}{-r+4.25}.\text{ What is the greatest possible value of }r\text{ such}\\&\text{that }w(r)=0?\end{aligned}\)

\(\begin{aligned}&~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~n(x)=2(x+8)+(x-8)\\&\text{The function }n\text{ is defined as shown.}\text{ For what value of }x \text{ is }n(x)=35?\end{aligned}\)

\(\text{The function }f\text{ is defined by }f(x)=5\left(\frac{1}{4}-x\right)^{2}+\frac{11}{4}.\text{ What is the value of }f\left(\frac{1}{4}\right)?\)

\(\begin{aligned}&\text{The function }f\text{ is defined by }f(x)=(-8)(2)^x+22.\text{ What is the }y\text{-intercept of the graph of }y=f(x)\\&\text{in the }xy\text{-plane?}\end{aligned}\)

\(\begin{aligned}
&\text{The function }f\text{ is defined by }f(x)=7x-84.\text{ What is the }x\text{-intercept of the graph of }\\&y=f(x)\text{ in the }xy\text{-plane?}\end{aligned}\)

\(\begin{aligned}
&~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~f(x)=5^x+3\\
&\text{If the given function }f\text{ is graphed in the }xy\text{-plane, where }y=f(x),\text{what is the }\\
&y\text{-intercept of the graph}?
\end{aligned}\)

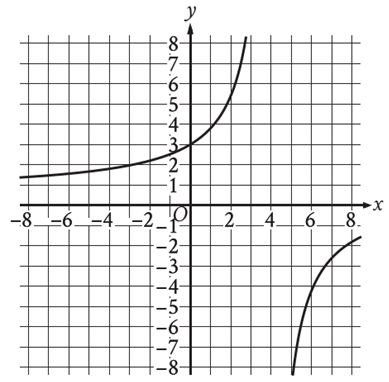
\(\text{The graph of }y=f(x)\text{ is shown in the }xy\text{-plane.}\text{ What is the value of }f(0)?\)

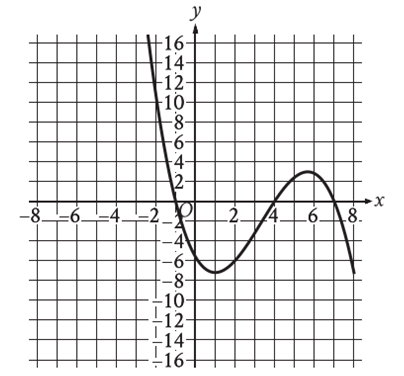
\(\begin{aligned}&\text{The graph of }y=f(x)\text{ is shown, where the function }f\text{ is defined by }f(x)=ax^{3}+bx^{2}+cx+d\\&\text{and }a,~b,~c,\text{ and }d\text{ are constants. For how many values of }x\text{ does }f(x)=0?\end{aligned}\)

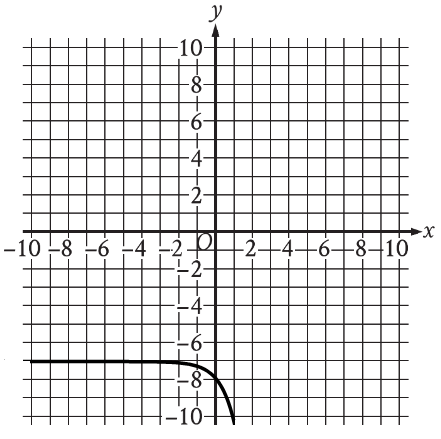
\(\begin{aligned}&\text{The graph of }y=f(x)\text{ is shown, where }f(x)=ab^x+c,\text{ and }a,~b, \text{ and } c\text{ are constants. For}\\
&\text{how many values of }x\mathrm{~does~}f(x)=0?\end{aligned}\)

\(\begin{aligned}
&~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~y=3\left (\frac{a}{6} \right)^{x+c}-b\\
&\text{How many times does the graph of the given equation in the }xy\text{-plane cross the }x\text{-axis,}\\
&\text{where }a,b\text{ and }c\text{ are positive constants such that }a > 6\text{ and }b > c?
\end{aligned}\)

\(\begin{aligned}
&\text{The function }T(x)=\frac{22,000-6.5x}{1,000}\text{ gives the estimated air temperature }T(x),\text{ in degrees}\\&\text{Celsius (°C), surrounding a hot air balloon at an altitude of }x\text{ meters. lf the estimated air}\\&\text{temperature surrounding the hot air balloon is }16°\text{C, which of the following is closest to the}\\&\text{altitude, in meters, of the hot air balloon?}\end{aligned}\)

\(\begin{aligned}&~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~C(t)=240\left(\frac{53}{52}\right)^{t-15}+7\\&\text{The function }C\text{ gives the estimated number of cephalopods, a class of marine animal, in a}\\&\text{certain area, where }t\text{ is the number of months since a study began. How many months after}\\&\text{the study began was the number of cephalopods in the area estimated to be 247?}\end{aligned}\)

\(\begin{aligned}
&\text{A beaker containing a liquid is placed on a table. The function}\\
&g(t)=294+(363-294)(2.72)^{-0.103t}\text{ gives the approximate temperature, in}\\
&\text{kelvins, of the liquid }t\text{ minutes after the beaker was placed on the table. According}\\
&\text{to this function, what was the approximate temperature, in kelvins, of the liquid}\\
&\text{when the beaker was placed on the table?}\end{aligned}\)

\(\begin{aligned}&~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~h(x)=x^{2}-3\\&\text{Which table gives three values of }x\text{ and their corresponding values of }h(x)\text{ for the given}\\&\text{function }h?\end{aligned}\)

\(\begin{aligned}&~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~q(x)=44(4^x)\\&\text{Which table gives three values of }x\text{ and their corresponding values of }q(x)\text{ for function }q?\end{aligned}\)

\(\text{If }h(x)=2^x\text{, what is the value of }h(5)-h(3)?\)

\(\begin{aligned}
&~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~f(x)=-0.0038400x^2+15.236x-15.103\\
&\text{The model shown gives the predicted average Arctic sea ice area }f(x),\text{ in}\\
&\text{millions of square kilometers, for September of each year }x,\text{ where }x\\
&\text{represents a year and }1979\leq x\leq2012.\text{ Based on the model, what is the}\\
&\text{positive difference, in millions of square kilometers, between the predicted}\\
&\text{average Arctic sea ice area for September of the year 1991 and the predicted}\\
&\text{average Arctic sea ice area for September of the year 1992? (Round your}\\
&\text{answer to the nearest thousandth.}\end{aligned}\)

\(\text{The function }f\text{ is defined by }f(x)=\left|x-4x\right|.\text{ What value of }a\text{ satisfies }f(5)-f(a)=-15?\)

\(\begin{aligned}&\text{The function }f\text{ is defined by }f(x)=\frac{|x|}{a}-14,\text{where }a < 0.\text{ What is the product of}\\&f(15a)\text{ and }f(8a)?\end{aligned}\)

\(\begin{aligned}
&\text{The function }k\text{ is defined by }k(s)=\sqrt{s+110}.\text{ If }k(53p)=p,\text{ where }p\text{ is a constant,}\\
&\text{What is the value of }p?\end{aligned} \)

\(\begin{aligned}
&\text{The function }g\text{ is defined as }g(x)=\frac{2x-4}{(x+11)(x-6)}.\text{ If }g(a+5)=0,\text{ where }a\text{ is a constant, }\\
&\text{what is the value of }a?\end{aligned}\)

\(\begin{aligned}
&\text{The linear function }g\text{ is defined by }g(x)=b-15x,\text{where }b\text{ is a constant. If }g(c+7)=\frac{c}{4},\\
&\text{where }c\text{ is a constant, which of the following expressions represents the value of }b ?\end{aligned}\)

\(\text {If }f(x)=x+2\text{ and }g(x)=2x\text{, what is the value of }3f(-5)-g(-5)?\)

\(\begin{aligned}&~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~f(x)=|71-2x|\\&\text{The function }f\text{ is defined by the given equation. For which of the following values of }k\\&\text{does }f(k)=3k?\end{aligned}\)

\(\begin{aligned}&~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~g(x)=\frac{2}{7}x+\frac{8}{5}\\&~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~h(x)=5x-7\\&\text{The functions }g\text{~and~}h\text{ are defined by the equations shown. Which expression is equivalent}\\&\text{to }g(x)\cdot h(x)?\end{aligned}\)

\(\begin{aligned}&~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~f(x)=x+4\\&~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~g(x)=3x^2-rx+48\\&\text{The functions }f\text{ and }g\text{ are given. In function } g,~r\text{ is a constant. If }\\&f(x)\cdot g(x)=3x^{3}+192,\text{ what is the value of }r?\end{aligned}\)

\(\begin{aligned}&~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~r(x)=5(x-2)\\&~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~s(x)=x^3+nx^2+2nx+8\\&\text{For the given functions }r\text{ and }s,~n\text{ is a constant. If }r(x)\cdot s(x)=5(x^4-16),\text{what is the}\\&\text{value of }n?\end{aligned}\)

\(\begin{aligned}&~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~f(x)=2x+3\\&~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~g(x)=7x-2\\&~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~h(x)=5x+6\\&\text{The functions }f,g,\text{ and }h\text{ are defined as shown. If }f(x)\cdot g(x)-h(x)=ax^2+bx+c,\\&\text{where }a,~b,\text{ and }c\text{ are constants, what is the value of }b?\end{aligned}\)

\(\begin{aligned}&\text{The functions }f\text{ and }g\text{ are defined as }f(x)=\frac{1}{5}x-9\text{ and }g(x)=\frac{4}{5}x+27.\text{ If the function }h\\&\text{is defined as }h(x)=f(x)+g(x),\text{ what is the }x\text{-intercept of the graph of }y=h(x)\text{ in the }xy\text{-}\\&\text{plane?}\end{aligned}\)

\(\begin{aligned}&~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~f(x)=7x-5\\&\text{Function }f\text{ is defined by the given equation. The function }g\text{ is defined by}\\&g(x)=f(x)-(5x-2).\text{ What is the }x\text{-coordinate of the }x\text{-intercept of the graph of}\\&y=g(x)\text{ in the }xy\text{-plane?}\end{aligned}\)

\(\begin{aligned}&~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~f(x)=5x-9\\&\text{Function }f\text{ is defined by the given equation. The function }g\text{ is defined by }\\&g(x)=f(x)-(3x-2).\text{ What is the }x\text{-coordinate of the~}x\text{-intercept of the graph of }\\&y=g(x)\text{ in the }xy\text{-plane?}\end{aligned}\)

\(\begin{aligned}
&\text{In the }xy\text{-plane, the point }(3, 6)\text{ lies on the graph of the function }f(x)=3x^{2}-bx+12.\\
&\text{What is the value of }b?\end{aligned}\)

\(\begin{aligned}
&~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~\begin{array}{|c|c|}\hline x&f(x)\\\hline-37&4\\\hline-9&0\\\hline33&6\\\hline\end{array}\\\\
&\text{The table shows three values of }x\text{ and their corresponding values of }f(x),\text{ where }\\
&f(x)=\frac{kx+45}{x+2}\text{ and }k\text{ is a constant. What is the value of }k?\end{aligned}\)

\(\begin{aligned}
&\text{For a particular car, the linear function }f\text{ gives the predicted power, in brake horsepower}\\
&\text{(bhp), for engine speeds between 1,000 revolutions per minute (rpm) and 6,000 rpm.}\\
&\text{According to this function, the car’s predicted power is 228 bhp at an engine speed of}\\
&\text{1,896 rpm and 600 bhp at an engine speed of 4,500 rpm. The equation}\\&
f\left(x\right)=\frac{1}{7}\left(x-a\right)+228\text{ defines }f,\text{where }x\text{ is the engine speed, in rpm, and }a\text{ is a constant}\\&\text{What is the value of }a?\end{aligned}\)

\(\begin{aligned}
&~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~g(x)=\frac{x^2-x-a}{x^2-x-b}\\
&\text{The function }g\text{ is defined by the given equation, where }a\text{ and }b\text{ are constants }f(x).\text{ In the }\\
&xy\text{-plane, the graph of }y=g(x)\text{ passes through the point }(0, 43)\text{, and }g(-43)=0.\text{ What is }\\&\text{the value of }b?\end{aligned}\)

\(\begin{aligned}
&\text{The function }f\text{ is defined by }f(x)=a^{x}-b,\text{ where }a\text{ and }b\text{ are constants. }\\
&\text{The graph of }y=f(x)\text{ in the }xy\text{-plane passes through the points }(0, -5)\\
&\text{and }(1, 2).\text{ What is the value of }a?\end{aligned}\)

\(\begin{aligned}
&\text{The function }f\text{ is defined by }f(x)=a^x+b\text{, where }a\text{ and }b\text{ are constants and }a>0.
\\&\text{In the }xy\text{-plane, the graph of }y=f(x)\text{ has a }y\text{-intercept at }(0,-20)\text{ and passes}\\&\text{through the point }(2,43).\text{ What is the value of }a-b?\end{aligned}\)

\(\begin{aligned}
&\text{The function }f\text{ is defined by }f(x)=a^x+b\text{, where }a\text{ and }b\text{ are constants and }a>0.
\\&\text{In the }xy\text{-plane, the graph of }y=f(x)\text{ has a }y\text{-intercept at }(0,-25)\text{ and passes}\\&\text{through the point }(2,23).\text{ What is the value of }a+b?\end{aligned}\)

\(\begin{aligned}
&~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~\begin{array}{|c|c|}\hline x&g(x)\\\hline-27&3\\\hline-9&0\\\hline21&5\\\hline\end{array}\\
&\text{The table shows three values of }x\text{ and their corresponding values of }g(x),\text{ where }g(x)=\frac{f(x)}{x+3}\\
&\text{and }f\text{ is a linear function. What is the }y\text{-intercept of the graph of }y=f(x)\text{ in the }xy\text{-plane?}\end{aligned}\)

\(\begin{aligned}
&~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~\begin{array}{|c|c|}\hline x&g(x)\\\hline-23&2\\\hline-9&0\\\hline19&4\\\hline\end{array}\\
&\text{The table shows three values of }x\text{ and their corresponding values of }g(x),\text{ where }g(x)=\frac{f(x)}{x+2}\\
&\text{and }f\text{ is a linear function. What is the }y\text{-intercept of the graph of }y=f(x)\text{ in the }xy\text{-plane?}\end{aligned}\)

\(\begin{aligned}
&~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~f(x)=\frac{3}{2}x+b\\
&\text{In the function above, }b\text{ is a constant. If }f(6)=7,\text{what is the value of }f(-2)?\end{aligned}\)

\(\begin{aligned}
&~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~g(x)=ax^2+24\\
&\text{In the function above, }a\text{ is a constant. If }g(4)=8,\text{what is the value of }g(-4)?\end{aligned}\)

\(\begin{aligned}&\text{The function }f\text{ is defined by }f(x)=(x-5)(x-8)(x+k),\text{ where }k\text{ is a constant. In}\\&\text{the }xy\text{-plane, the graph of }y=f(x)\text{ passes through the point }(-2,0).\text{ What is the value of}\\&f(0)?\end{aligned}\)

\(\begin{aligned}&\text{The function }h\text{ is defined by }h(x)=(x+p)(x-2)(2x-12),\text{ where }p\text{ is a constant. In}\\&\text{the }xy\text{-plane, the graph of }y=h(x)\text{ passes through the point }(-3,0).\text{ What is the value of}\\&h(0)?\end{aligned}\)

\(\begin{aligned}
&\text{The function }g\text{ is defined by }g(x)=(x+14)(t-x),\text{ where }t\text{ is a constant. In the }xy\text{-plane,}\\
& \text{the graph of }y=g(x)\text{ passes through the point }(24,0).\text{ What is the value of }g(0)?\end{aligned}\)

\(\begin{aligned}
&\text{The function }f\text{ is defined by }f(x)=4(x-3)(x^2-k),\text{ where }k\text{ is a constant. In the }xy\text{-plane,}\\
&\text{the graph of }y=f(x)\text{ passes through the point }(-8,0).\text{ What is the value of }f(0)?\end{aligned}\)

\(\begin{aligned}
&\text{The exponential function }g\text{ is defined by }g(x)=19\cdot a^{x},\text{ where }a\text{ is a positive constant. If}\\
&g(3)=2,375,\text{ what is the value of }g(4)?\end{aligned}\)

\(\begin{aligned}
&\text{The function }v\text{ is defined by the equation }v(x)=\frac{x^2+bx+c}{(x+5)(x-19)},\text{ where }b\text{ and }c\text{ are constants.}\\
&\text{In the }xy\text{-plane, the graph of }y=v(x)\text{ passes through the points }\left(0, ~\frac{66}{95}\right)\text{and }(11,0).\text{ If}\\&v(q)=0,\text{ which of the following could be the value of }q?\\
\end{aligned}\)

\(\begin{aligned}
&\text{The function }p\text{ is defined by }p(x)=a\left(\left(x+6\right)^2-b\right)\left(\left(x+6\right)^2-c\right),\text{where }a,b,\text{ and }c\text{ are}\\&\text{constants. In that }xy\text{-plane, the graph of }y=p(x)\text{ passes through the points }(-7,24)\text{ and}\\&(0,899).\text{What is the value of }p(-12)+p(-5)?\end{aligned}\)

\(\begin{aligned}&\text{The function }q\text{ is defined by }q(x)=a|x-9|^2-87|x-9|+b,\text{ where }a\text{ and }b\text{ are constants,}\\&\text{and }a>b>87.\text{ If }q(639)=h\text{ and }q(-621)=k,\text{ where }h\text{ and }k\text{ are constants, what is the}\\&\text{value of }9(-639)^{h-k}+621(9)^{k-h}?\end{aligned}\)

\(\begin{aligned}&\text{An exponential function }f\text{ is defined by }f(x)=c^x,\text{where }c\text{ is a constant greater than }1.\text{ If}\\&f(7)=9\cdot f(5),\text{what is the value of }c?\end{aligned}\)

\(\begin{aligned}
&\text{The functions }g\text{ and }h\text{ are defined by the given equations.}\\
&~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~g(x)=\sqrt{(x-11)^{2}+45}\\
&~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~h(x)=\sqrt[3]{64}+\frac{x^{2}}{2}\\
&\text{If the value of }g(8)=t,\text{ where }t\text{ is a constant, what is the value of }h(t)?\end{aligned}\)

\(\begin{aligned}
&\text{The function }f\text{ is defined by }f(x)=a\sqrt{b-x},\text{where }a\text{ and }b \text{ are constants.}\\
&\text{In the }xy\text{-plane, the graph of }y=f(x)\text{ passes through the point }(22, 0),\\
&\text{and }f(-22) <0.\text{ Which of the following must be true?}
\end{aligned}\)

\(\begin{aligned}&\text{The function }h\text{ is defined by }h(x)=-\sqrt{x^2+bx+c}\text{ , where }b\text{ and }c\text{ are constants. In}\\&\text{the }xy\text{-plane, the graph of }y=h(x)\text{ contains the points }(2,0)\text{ and }(0,-\sqrt{334}).\text{ If }\\&h(m)=0,\text{ what is the greatest possible value of }m?\end{aligned}\)

\(\begin{aligned}&~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~f(x)=6(g(x))-3\\&~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~g(x)=|12x-7|\\
&\text{The functions }f\text{ and }g\text{ are defined by the given equations. What is the value of }f(-10)?\end{aligned}\)